Vsebina

• Koraki
• Nasvet

Če ste matematik ali grafični programer, boste morda morali najti kot med dvema danima vektorjema. V tem članku wikiHow prikazuje, kako to storiti.

Koraki

1. del 2: Poiščite kot med dvema vektorjema

1. 

   Opredelitev vektorja. Zapišite si vse informacije o dveh vektorjih, ki jih imate. Recimo, da imate samo določene parametre njihovih dimenzijskih koordinat (imenovane tudi komponente). Če že veste dolžino (velikost) vektorja, lahko preskočite nekaj spodnjih korakov.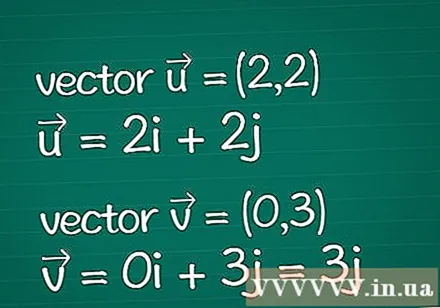
   • Primer: dvodimenzionalni vektor = (2,2) in dvodimenzionalni vektor = (0,3). Zapišemo jih lahko tudi kot = 2jaz + 2j in = 0jaz + 3j = 3j.
   • Čeprav so v primeru iz tega članka uporabljeni dvodimenzionalni vektorji, lahko naslednja navodila veljajo za vektorje s poljubnim številom dimenzij.

2. 

   
   
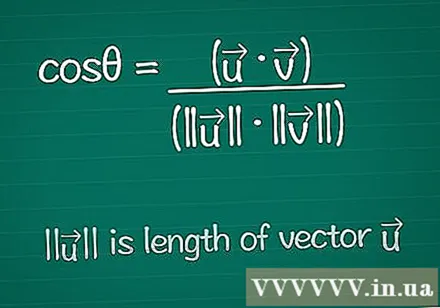
   Zapišite formulo kosinusa. Za iskanje kota θ med dvema vektorjema začnemo s formulo za iskanje kosinusa za ta kot. O tej formuli se lahko naučite spodaj ali pa jo preprosto zapišete tako:
   • cosθ = (•) / (|||| ||||)
   • |||| pomeni "dolžina vektorja".
   • • je skalarni zmnožek obeh vektorjev - to bo razloženo v nadaljevanju.

3. 

   
   
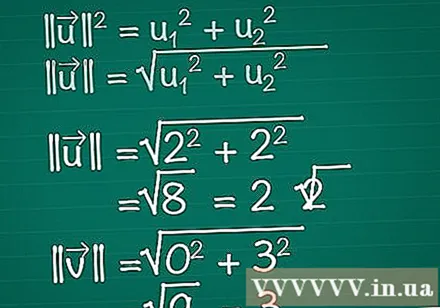
   Izračunajte dolžino vsakega vektorja. Predstavljajmo si, da je pravokotni trikotnik sestavljen iz komponent x, y vektorja in samega vektorja. Vektor tvori hipotenuzo trikotnika, zato za iskanje njegove dolžine uporabimo Pitagorin izrek. Pravzaprav je to formulo mogoče enostavno razširiti na vektor poljubnega števila dimenzij.
   • || u || = u₁ + u₂. Če ima vektor več kot dva elementa, morate še naprej dodajati + u₃ + u₄ +...
   • Zato je za dvodimenzionalni vektor || u || = √ (u₁ + u₂).
   • V tem primeru je |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
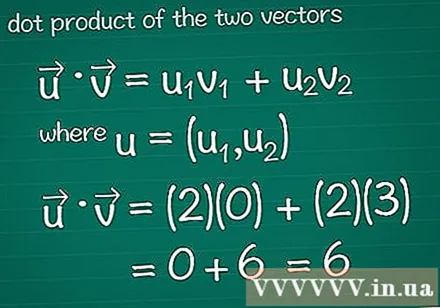
   Izračunaj skalarni zmnožek dveh vektorjev. Morda ste se naučili metode množenja vektorjev, znane tudi kot skalar to. Če želite izračunati skalarni izdelek glede na njegovo sestavo, sestavine pomnožite v obe smeri in nato seštejte celoten rezultat.
   • Za grafični program glejte Nasveti, preden nadaljujete z branjem.
   • V matematiki • = u₁v₁ + u₂v₂, kjer je u = (u₁, u₂). Če ima vektor več kot dva elementa, preprosto dodajte + u₃v₃ + u₄v₄...
   • V tem primeru je • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. To je skalarni zmnožek vektorja in vektorja.

5. 

   Rezultate dajte v formulo. Ne pozabite, da je cosθ = (•) / (|||| || ||). Zdaj poznamo skalarni zmnožek in dolžino vsakega vektorja. Vnesite jih v formulo za izračun kosinusa kota.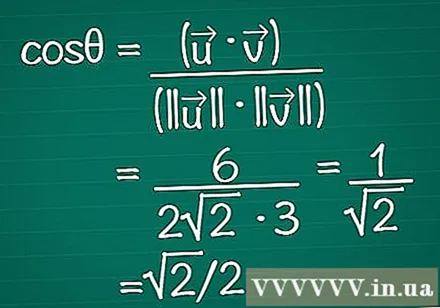
   • V našem primeru je cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Poiščite kot glede na njegov kosinus. Funkcijo arccos ali cos v kalkulatorju lahko poiščete θ iz znane vrednosti cos. Pri nekaterih rezultatih boste morda našli kot glede na enoto kroga.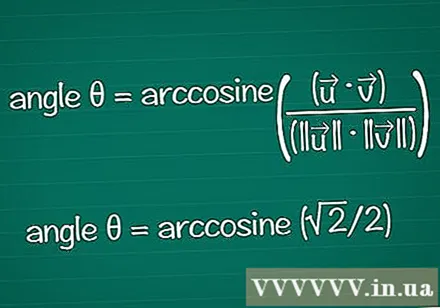
   • V primeru je cosθ = √2 / 2. V kalkulator vnesite "arccos (√2 ​​/ 2)", da poiščete kot. Ali pa lahko najdete kot θ na enoti kroga v položaju cosθ = √2 / 2. Velja za θ = /₄ ali 45º.
   • Končna formula je tako, da združimo vse: kot θ = arccosine ((•) / (|||| || ||))
   oglas

Del 2 od 2: Določitev formule kota

1. 

   Razumevanje namena formule. Ta formula ni izhajala iz obstoječih pravil. Namesto tega se oblikuje kot definicija skalarnega produkta in kota med vektorjema. Kljub temu ni šlo za samovoljno odločitev. Če se vrnemo k osnovni geometriji, lahko razumemo, zakaj ta formula ponuja intuitivne in uporabne definicije.
   • Spodnji primeri uporabljajo dvodimenzionalne vektorje, ker jih je najlažje razumeti in najenostavnejši. Tridimenzionalni ali več vektorjev imajo lastnosti, opredeljene s skoraj podobnimi splošnimi formulami.

2. 

   Preglejte Cosineov izrek. Razmislimo o navadnem trikotniku s kotom θ med stranicama a in b, nasproti strani c. Cosinov izrek pravi, da je c = a + b -2abcos(θ). Ta rezultat izhaja preprosto iz osnovne geometrije.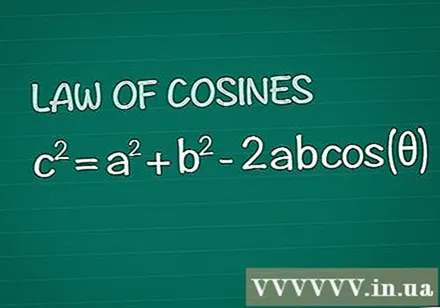

3. 

   Povežite dva vektorja, ki tvorijo trikotnik. Na papir narišite par dvodimenzionalnih vektorjev, vektorjev in vektorjev, pri čemer je θ kot med njimi. Med njima narišite tretji vektor, da ustvarite trikotnik. Z drugimi besedami, nariši vektor tako, da je + =. Vektor = -.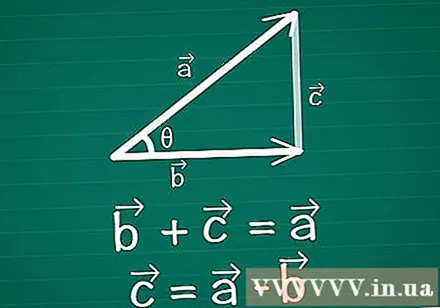

4. 

   Zapiši Cosineov izrek za ta trikotnik. Nadomestite stransko dolžino našega "vektorskega trikotnika" v Cosineov izrek:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Prepišite s skalarnim izdelkom. Ne pozabite, da je skalarni izdelek podoba enega vektorja na drugem. Skalarni zmnožek vektorja samega po sebi ne zahteva projekcije, ker tu ni razlike v smeri. To pomeni • = || a ||. S tem zapišemo enačbo:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Uspešno smo napisali isto formulo. Razširite levo stran formule in nato poenostavite, da dobite formulo za iskanje kotov.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   oglas

Nasvet

• Če želite spremeniti vrednosti in hitro rešiti težavo, uporabite to formulo za kateri koli par dvodimenzionalnih vektorjev: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Če delate s programsko opremo za računalniško grafiko, je verjetno, da boste morali skrbeti le za dimenzijo vektorjev, ne da bi skrbeli za njihovo dolžino. Za skrajšanje enačbe in pospešitev programa uporabite naslednje korake:
  • Normalizirajte vsak vektor tako, da je enak 1. Če želite to narediti, delite vsako komponento vektorja na njegovo dolžino.
  • Pridobite normaliziran zmnožek skalarja namesto prvotnega vektorja.
  • Ker je dolžina 1, lahko elemente dolžine izključimo iz enačbe. Na koncu dobljena enačba kota je arccos (•).
• Na podlagi kosinusne formule lahko hitro ugotovimo, ali je kot oster ali nejasen. Začnite s cosθ = (•) / (|||| ||||):
  • Leva in desna stran enačbe morata imeti enak predznak (pozitiven ali negativen).
  • Ker je dolžina vedno pozitivna, mora imeti cosθ enak znak kot skalarni zmnožek.
  • Če je izdelek pozitiven, je tudi cosθ pozitiven. Nahajamo se v prvem kvadrantu enotnega kroga z θ <π / 2 ali 90 °. Kot, ki ga najdemo, je oster kot.
  • Če je skalarni zmnožek negativen, je cosθ negativen. Nahajamo se v drugem kvadrantu enotnega kroga z π / 2 <θ ≤ π ali 90º <θ ≤ 180º. To je vogal zapora.